Recently, I've been thinking about grid coordinates in n-dimensional systems. When I first encountered a problem that required the generation of the lattice coordinates in n-space I was temporarily stumped. I was unsure of how to write an algorithm that can generate all points as a function of the dimension and the length of the cube. Previously, I always knew what dimensions I was working in and creating the coordinates of a cube of length N in for example three dimensions simply came down to nested loops:

coordinates = []
for i in range(length):
    for j in range(length):
        for k in range(length):
            coordinates += [(i,j,k)]        

This algorithm generates all of the lattice coordinates of a cube in three dimensions. However, it is limited to just that. Since I wanted a more robust algorithm that would return all coordinates based on the length as well as the dimension, I started to to think about approaching this problem from a different angle. Considering cube of length N in d-dimensional space, I calculated the total number of points in the cube as N**d. Now instead writing nested loops (one for each dimension) I simply looped from the variable point from 0 to N**d. By changing the value of point from base 10 to the base N I obtained all possible lattice coordinates. This works because in a cube of length N the only possible coordinate values are 0,1,...,n-1. The algorithm loops through all possible coordinates until it reaches N**d-1 which is equivalent to (N,N,...,N) in base N.

points = N**d
coordinates =[]
for point in xrange(points):
    cord = ()
    for dimension in range(d-1,-1,-1): 
        N_d = N**dimension
        if N_d<=p:
            cord += (point//N_d,)
            point=point%N_d
        else:
            cord += (0,)
    coordinates += [cord]

Executing this code for d=3 and n=3 yields the following coordinates below. However, what has really happened here is that we converted a decimal numbers into base N numbers.

[(0, 0, 0), (0, 0, 1), (0, 0, 2), (0, 1, 0), (0, 1, 1), (0, 1, 2), (0, 2, 0), (0, 2, 1), (0, 2, 2), (1, 0, 0), (1, 0, 1), (1, 0, 2), (1, 1, 0), (1, 1, 1), (1, 1, 2), (1, 2, 0), (1, 2, 1), (1, 2, 2), (2, 0, 0), (2, 0, 1), (2, 0, 2), (2, 1, 0), (2, 1, 1), (2, 1, 2), (2, 2, 0), (2, 2, 1), (2, 2, 2)]

Next, I wanted to extend this idea into shells around the origin (0,0,...,0). In the previous example, the origin was in the corner of the cube. We now want to move it to the center. This is accomplished by subtracting N//2 from each coordinate where N is the width of the shell that the particular point is a part of. First I create origin which has a width of 1, the first shell has a width of 3 followed by a width of 5. Thus, the width of the shells is given by 2*n+1 where n is the shell number. Again, I considered a cube of length N in d dimensions.

shells = []
for N in range(1,N+1,2):
    cords = []
    points = N**d
    for point in xrange(points):
        cord = ()
        for dimension in range(d-1,-1,-1):
            N_d = N**dimension
            if N_d<=point:
                cord += (point//N_d-N//2,)
                point=point%N_d
            else:
                cord += (0-N//2,)
        coordinates += [cord]
    if len(shells)>0:
        for i in range(len(shells)):
            coordinates = list(set(coordinates)-set(shells[i]))
        shells+=[coordinates]
    else:
        shells += [cords]

Not much has changed except for the movement of the origin and building up full shells. The results for the first two shells in 2 dimensional space are:

Core:
[(0, 0)]
Shell:  1
[(0, 1), (-1, 1), (-1, 0), (-1, -1), (0, -1), (1, 0), (1, -1), (1, 1)]
Shell:  2
[(1, 2), (-2, 2), (-2, 1), (-1, 2), (-2, 0), (2, 2), (2, -1), (-1, -2), (2, 1), (-2, -1), (2, 0), (2, -2), (-2, -2), (0, -2), (1, -2), (0, 2)]

Everything looks good! Lets plot the results from N=1,2,3 and d=2 points to verify we have really obtained the correct points for each shell:

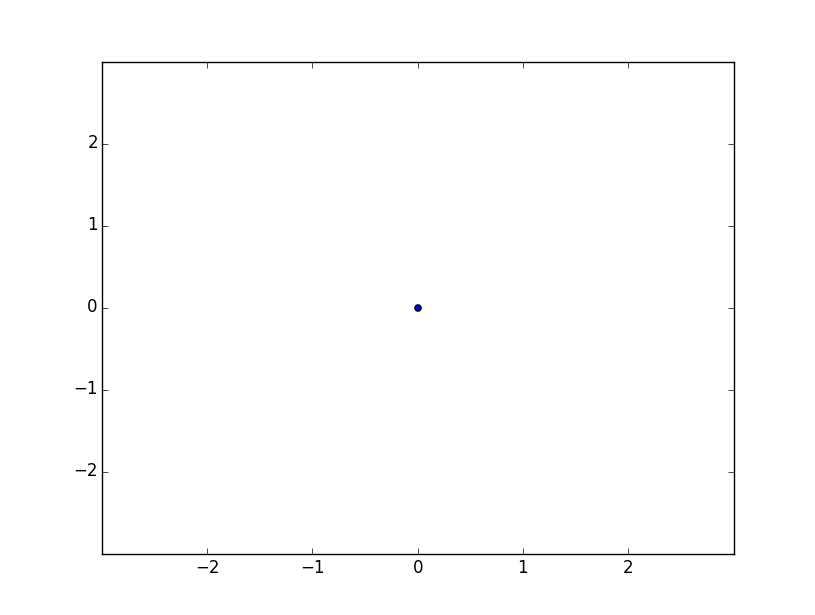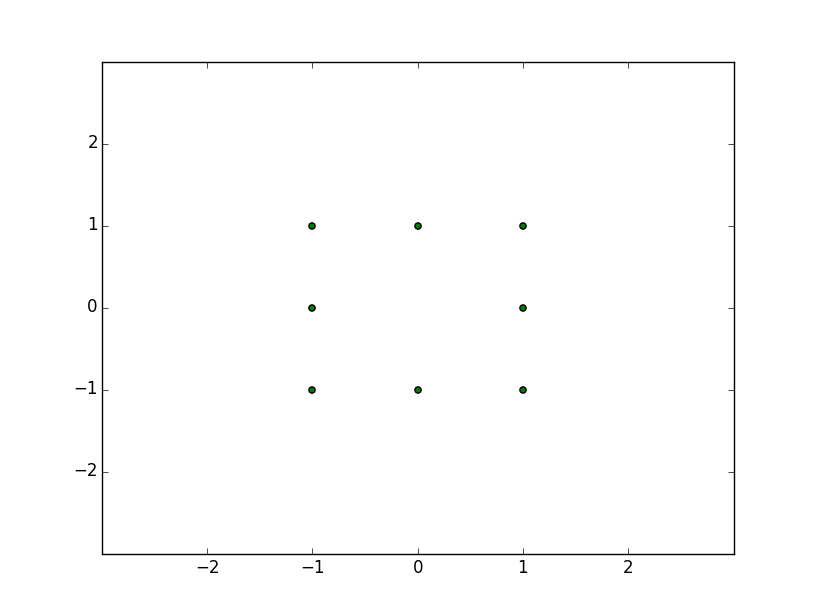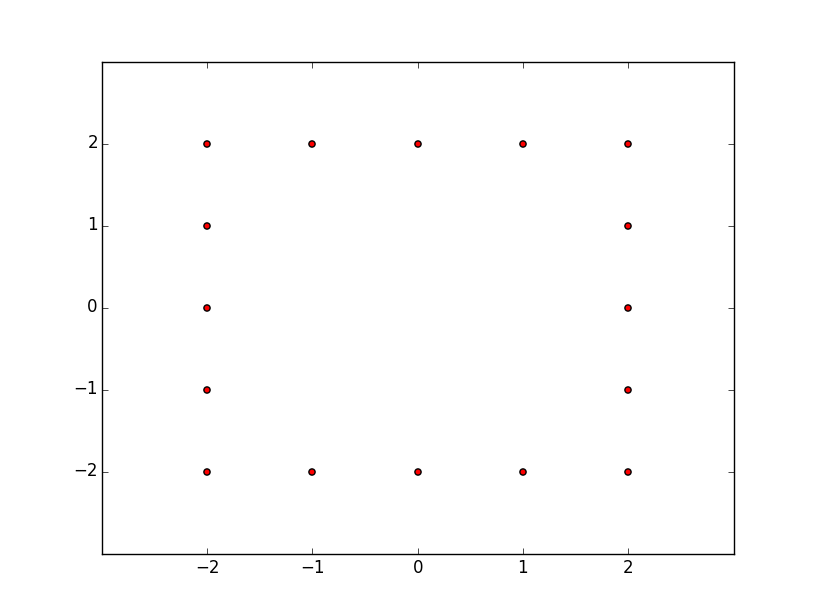
And N=1,2,3 and d=3:

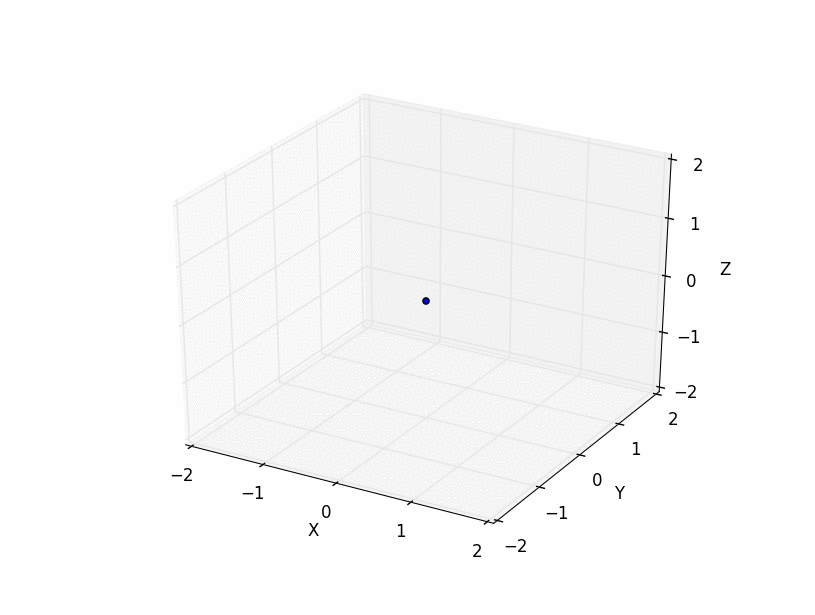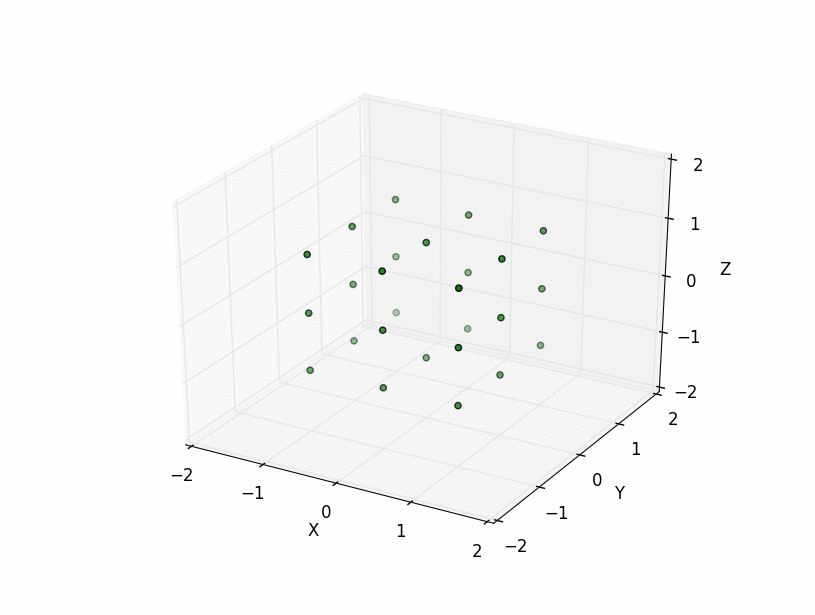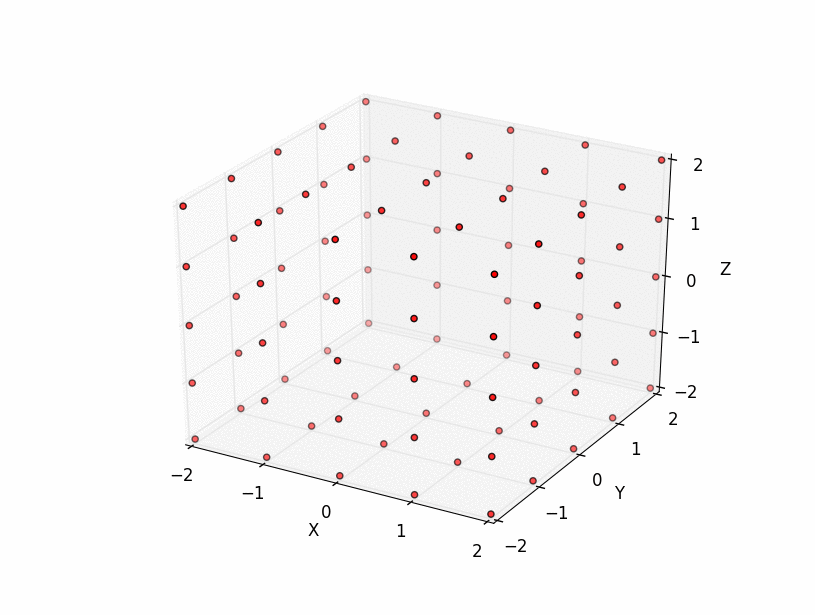
These plots show that this algorithm produces the shells of a cube in 2 and 3-D. Coordinates in higher dimensions are also correctly reproduced but are very difficult to visualize with plots. Currently, the code is fairly inefficient as it reproduces all coordinates for each shell. I will think about whether there is a good way of producing just the shell coordinates later.